2023.6.1(목)에 시행되는 2024학년도 6월모의평가에 앞서 2022학년도에 시행된 2023학년도 6월모의평가의 미적분 30번 문항을 풀이해보고자 합니다. 수학 공부를 할 때 가장 중요한 것은 주어진 문제를 해결하는데만 목적을 두는 것이 아니라 그 문제로 부터 배워가야할 것들을 배워가는데 목적을 두어야 합니다. 바로 풀이 시작하겠습니다.
먼저 문제를 살펴볼게요.

위 사진에서 넘버링되어 있는 조건들을 살펴보겠습니다.
1. 일단 주어진 곡선 f(x)를 미분을 이용하여 그릴 수 있어야 합니다. 자세한 그림은 밑에서...
2. 이 부분을 해석하면 곡선 y=f(x)와 y=f(x) 위의 점 (t, f(t))에서의 접선 y=f’(t)(x-t)+f(t)의 교점의 개수를 g(t)로 둔 것이라고 해석해야 합니다. 수능 문제에서 실근의 개수를 묻는 대부분의 문제는 교점의 개수로 접근합니다.
3. g(t)는 교점의 개수를 나타내는 함수로 함숫값으로 자연수만을 가질 수 있습니다.
(접점이 항상 존재하므로 함숫값이 0일 수는 없습니다.)
따라서 t=5에서 g의 함숫값과 극한값의 합은 1+4, 2+3, 3+2, 4+1 중 하나입니다.
즉, t=5에서 함숫값과 극한값은 다르며, t=5에서 g는 불연속입니다.
4.이 식을 해석하면 g(t)는 t=k에서 좌극한과 우극한이 다르며, 불연속입니다.
이제 함수 f(x)와 g(t)를 그려보겠습니다.
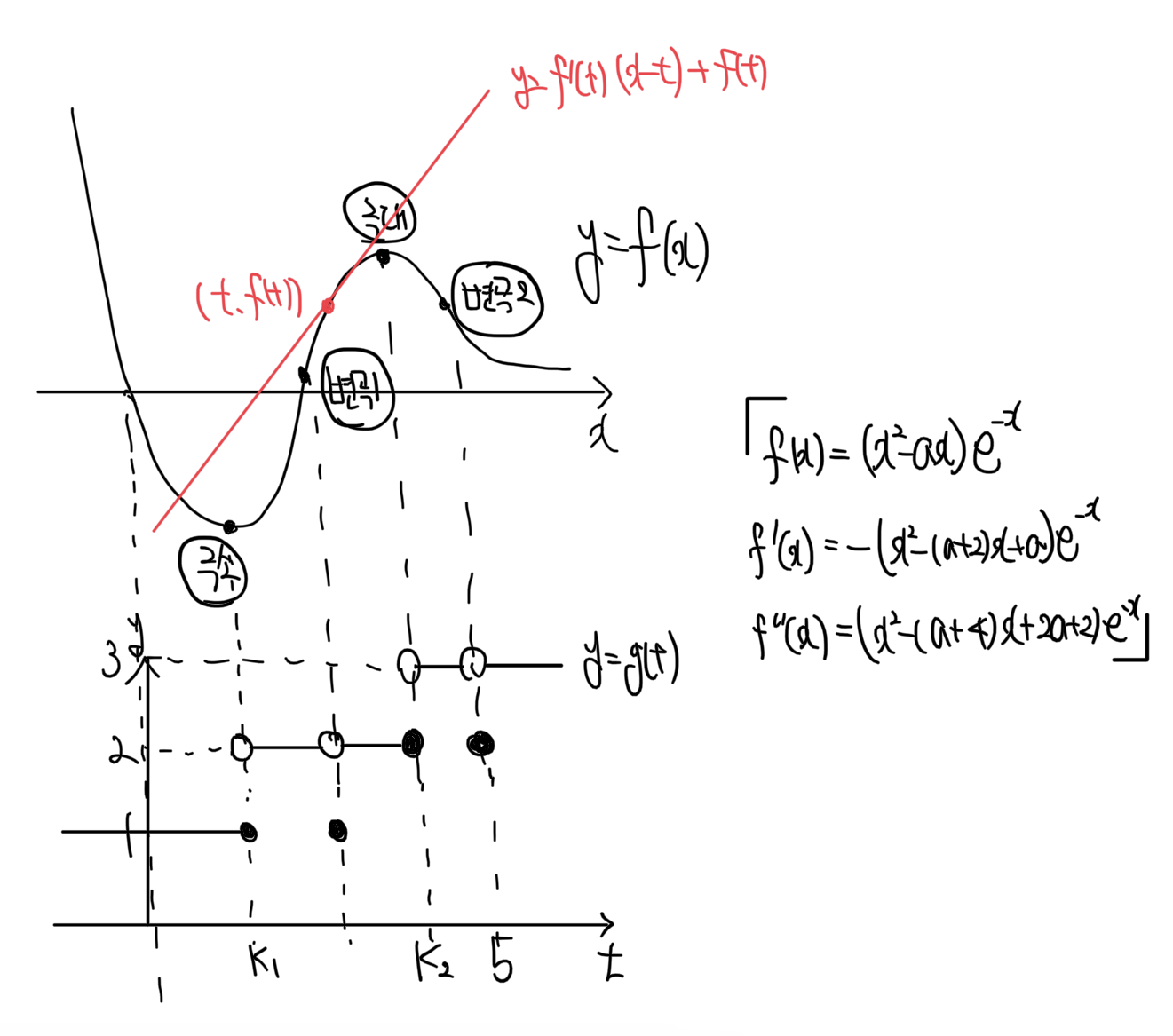
f(x) 위의 점 (t,f(t))에서 t 값을 오른쪽으로 이동하면서 접선과 곡선의 교점의 개수를 세면, g(t) 그래프를 그림과 같이 완성할 수 있습니다.
★ 여기서 꼭 배워가야 하는 개념은 변곡점 위에서 접선을 그었을 때 변곡점 주변의 위로볼록, 아래로볼록인 영역과는 교점이 생기지 않는다는 것입니다. 이제 그림에 대한 설명을 덧붙여보겠습니다.
첫째, 그래프에서 g(t)의 함숫값과 극한값의 합이 5가 되는 점은 f의 변곡점2에 해당하는 t값으로 변곡점2에서 t=5임을 확인할 수 있습니다. 즉 f’’(5)=0임을 알 수 있습니다. 이를 이용하면, a=7/3 이라는 것을 구할 수 있습니다.
둘째, 그리고 g(t)의 불연속점 중 좌극한과 우극한이 다른 점은 f의 극솟값과 극댓값에 해당하는 두 개의 t값뿐임을 확인할 수 있습니다. 각각 그림에서 t=k1, t=k2입니다. 또한 k1과 k2는 극소와 극대를 만드는 x값이므로 f’(t)=0의 해라는 걸 알 수 있습니다.
f’(t)=-(x^2-(a+2)x+a)e^-x 이므로 f’(t)=0의 해는 x^2-(a+2)x+a=0의 두 해만 존재하고
그 해가 k1과 k2인 것이죠. 따라서 조건을 만족하는 모든 k의 합은 k1+k2이고, 이차방정식의 근과 계수와의 관계에 의하여 k1+k2=a+2=7/3+2=13/3 이 됩니다.
따라서 p=3, q=13이므로 p+q=16이 됩니다.
이 부분을 식으로 나타내면 다음과 같습니다.
미적분 30번 문제인만큼 쉽지는 않습니다. 쉽지 않은 만큼 풀이를 이해하려는 과정에서 얻어갈 것이 많은 문제입니다. 특히 주어진 조건들을 해석하는 부분을 눈여겨 보면 좋을 것 같아요. 문제가 주어졌을 때 무턱대고 달려드는 것보다는 꼭 조건 분석해보고 접근하는 것을 추천합니다.
블로그에서 수학 풀이를 한다는 것이 굉장히 어렵네요. 풀이에 질문이 있다면 댓글 달아주세요.
'수능 수학 공부 비법' 카테고리의 다른 글
| 고등학생 여름방학 공부, 계획, 공부법, 공부방법(고1, 고2, 고3) (0) | 2023.07.19 |
|---|---|
| [수학 공부]2024학년도 6월모의고사 수학영역 미적분 30번 문항 풀이 (0) | 2023.06.02 |
| 고3 공부, 아는 것과 모르는 것 구분해서 공부하기 (4) | 2023.05.26 |
| 기말고사, 고3 내신 공부 하는 만큼 오르는 방법 (0) | 2023.05.25 |
| [수학 공부 비법] 수학 시험에서 실수하지 않는 법 (0) | 2023.03.31 |




댓글